
“La naturaleza de la unidad que existe en la vida procura expandirse en armonía tanto en el cosmos como en todo y cualquier ser individual”
Nilakanta Sri Ram en el libro “Seeking Wisdom”
Cuando Platón, en la República, dijo que los guardianes de ésta debían estudiar Geometría, para aprender a dirigir su espíritu a la contemplación de la Idea del Bien, ya que esta ciencia tiene por objeto “el conocimiento de lo que es siempre, y no de lo que nace y muere”, insinuó así, quizás, que las verdades de la geometría son verdades de la conciencia humana, producen en ella ecos y semejanzas que le despiertan del sueño de la materia en que vive.
Dado que los primeros símbolos son los números y las figuras geométricas, las relaciones de éstas conforman un lenguaje silencioso que despierta intuiciones en el alma, más allá de los juegos racionales que con las mismas se puedan hacer.
Un ejemplo de figuras geométricas que han tentado poderosamente a los investigadores, y que, más allá de sus aplicaciones prácticas en Óptica, Acústica, etc., llaman la atención de quien las estudia, son, sin duda, las cónicas. Las figuras que nacen de secciones del cono cortado por un plano: elipses, parábolas e hipérbolas.
En las tradiciones mistéricas se afirma que el Cono es la figura símbolo que representa el alma y evolución de todo lo que vive en la naturaleza, y de lo que en la India llaman Línea Dévica, que conforma a todos los espíritus rectores de la misma. Del mismo modo que la Pirámide lo es de la evolución de la conciencia humana.
Las secciones del cono serán, así, verdades intrínsecas del Alma de la Naturaleza, y dichas cónicas deben evocar profundas reflexiones en quien a ellas se acerque.
En la novela “Viaje Iniciático de Hipatia” dediqué varias páginas de explicaciones de la filósofa alejandrina sobre los misterios de las cónicas, recreadas, evidentemente con la imaginación, aunque sí se sabe que ella escribió un tratado matemático sobre las mismas.
Muchos geómetras estudiaron estas figuras, desde Menecmo, discípulo de Platón, Apolonio de Perga, Euclides, Arquímedes, entre los griegos, y luego el filósofo Pascal o Descartes y el mismo Kepler o Newton para explicar los movimientos celestes, y un largo etcétera.
En 1822, Germinal Pierre Dandelín (1794-1847) un matemático que había servido heroicamente bajo las banderas napoleónicas, encontró la llave que permitió abrir una puerta hasta entonces cerrada sobre estas mismas cónicas, el llamado teorema de las esferas de Dandelín. En este teorema demuestra que cuando una cónica es generada al ser cortado el cono por un plano, los focos de esta cónica van a ser los puntos en que dos esferas inscritas en el mismo cono y tangentes al mismo, tocan en un punto a dicho plano (o sea, que el plano que genera la cónica es también tangente a dichas esferas)
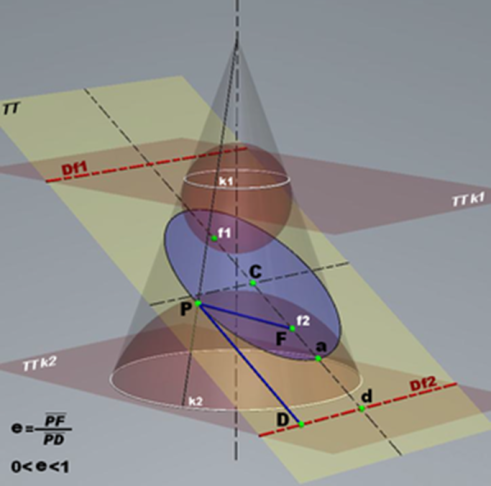
Veámoslo con una imagen, y aplicada al ejemplo concreto de la elipse
La demostración, muy elegante, de este teorema y explicación de sus detalles podemos verla, por ejemplo, de forma magistralmente pedagógica en el canal de youtube 3Blue1Brown, de Grant Sanderson[1] en este video, que se llama, curiosamente, “Cómo convertir a quien aún no sea, amante de la matemática”
Vemos en el diagrama claramente cómo en el interior del cono hay dos esferas (de la más baja sólo se ve la mitad) tangentes a sus paredes, una justo encima y la otra debajo, y ambas tangentes al plano que genera la elipse (en azul), exactamente en los puntos de los focos de la misma (f1 y f2).
Recordemos que en la elipse, la suma de las distancias desde cualquier punto de la misma a los dos focos es constante. La excentricidad de la elipse viene dada por la inclinación del plano que intersecta el cono, o, matemáticamente hablando, la razón entre la distancia de los focos y la longitud del eje mayor de la elipse. Por eso sus valores van entre cero (nula excentricidad, que define la circunferencia) y 1 (que sería ya una línea de ida y retorno).
Si consideramos que puntos y esferas son símbolos de unidad, el punto unidad en lo infinito, y la esfera, unidad plasmada en la armonía de aquello que contiene o de lo que expresa; podemos pensar en el cono, como una sucesión infinita de esferas que se alejan de la unidad vértice del cono que las generó. Los centros de estas esferas, que van perdiendo la luz de su unidad raíz (vértice del cono) están en el eje del cono, como si dichos centros fueran la proyección de esta “unidad en el misterio” (pues se halla fuera de la esfera), pero contenidas aún en el cono-realidad vital que genera -en su ley, por tanto- representada por las paredes del cono.
En cierto modo, cada esfera es un mundo, una realidad propia, una existencia, siempre relativas, pues su “centro emisor” es sólo un eco de la unidad raíz, a la una le sucede la siguiente en el proceso de expansión del cono, que puede simbolizar, como dice Plotino, la entrada de la Luz del Ser en la materia, que es, simplemente, alejamiento de la Unidad.
El plano que corta el cono por entero, genera una elipse. El plano es, en este caso, el instante presente, el aquí y ahora, una fotografía de ese proceso dinámico del cono. Es la vida, que respira siempre en el presente. Y sin embargo, siempre hay dos esferas-mundos que la generan, más o menos alejadas según la inclinación del plano que corta el cono. El foco de la elipse que es un centro de irradiación y fuerzas desde la esfera superior, bien podemos llamarlo “futuro”, ideal, deber ser, la puerta abierta a las esperanzas, el cielo, regreso a la unidad; y el foco que lo es desde la inferior, el pasado, las raíces, la tierra, el recuerdo. El aquí y el ahora del presente, gira siempre movido por esas dos fuerzas que traccionan de él.
Y quien dice pasado y futuro, dice materia y esa “materia más refinada” que llamamos espíritu, o espíritu y ese espíritu más lentificado que llamamos materia. Como diría Platón, todo lo que existe es hecho de lo Uno y de lo Otro.
Tal como dice Grant Sanderson, las “Esferas de Dandelin” han permitido explicar de un modo mucho más pedagógico y fácil el hecho de que una elipse sea al mismo tiempo:
- Una circunferencia “estirada” o deformada en uno de los ejes.
- La sección de un cono con un plano que la corta en un ángulo no superior al de la generatriz,
- El lugar geométrico de los puntos cuyas distancias a los focos suman una constante.
Más adelante este matemático, Dandelin, abstraería este teorema del cono a todo hiperboloide de revolución.
Y aunque el teorema de las Esferas-Focos es su contribución más recordada, también se adentró en métodos numéricos para solucionar ecuaciones algebraicas, en proyecciones esterográficas, en teoría de probabilidad y en álgebra.
Así, gracias a su visión, se halla un sentido a estos focos de la elipse, que la definían, pero que de ellos mismos no se sabía la procedencia. Nacen de las tangentes de la esfera, en este caso, de dos esferas. Al final, como decía Parménides, la Esfera está detrás de todas las cosas, sea que la veamos cóncava desde el interior, la realidad del sujeto en el interior de su propia irradiación, o convexa en los infinitesimales átomos o grandiosos mundos de lo que constituye la realidad como objeto.
Jose Carlos Fernández