[vimeo]https://vimeo.com/15386378[/vimeo]

Soy matemática. Lo sé, lo he dicho muchas veces. Si encima fuera de Bilbao no habría quien me aguantase. Afortunadamente para vosotros, soy sevillana y no me consta tener ningún apellido vasco. Como se cuenta en mi perfil, yo lo que quería era llenar estadios de gente que gritara y bailara al ritmo que yo les marcara, como una diva de la canción, pero como mi familia no tenía suficiente pasta para asumir el riesgo de mi carrera artística y puesto que las matemáticas siempre me habían fascinado en el instituto, decidí estudiar eso, matemáticas. Mucha gente no entiende este tipo de decisiones, pero siempre fui temeraria. Me gustaba provocar. Pero mucha menos gente entiende cuando le dices que investigas en matemáticas, ¿no está todo ya resuelto? ¿Van a cambiar las tablas de multiplicar? ¿Para qué sirve la investigación en matemáticas?

Normalmente a la última de las cuestiones respondo, dependiendo de las condiciones de contorno en que se me formule, usando argumentos que se ajusten a la cotidianeidad de mi interlocutor. Google funciona siempre. «Sin matemáticas no existiría Google» es una respuesta bastante convincente. Pocos se quedan a escuchar cuando sigo hablando de matrices, autovectores y autovalores y su importancia en los algoritmos del citado buscador. Pero yo creo que se quedan bastante convencidos. O eso quiero pensar.

Pero en estos días, lamentablemente, la crisis del ébola nos da más argumentos para explicar para qué sirven las matemáticas y tratar de hacer apología de las mismas, sin más interés que concienciar a la sociedad de la necesidad de una buena formación en esta materia para entender el mundo.

Es justo (y necesario) que la población mundial esté preocupada por este nuevo brote de ébola. Sí, necesario para que se tomen todas las precauciones posibles sin llegar al histerismo. Pero en nuestro amado país, las conversaciones sobre el ébola, la mayoría, tienen que ver con la gestión, mejor dicho, la no gestión por parte de una absoluta incompetente (y todos los que trabajan para ella en su ministerio) y un desgraciado consejero que ha sido capaz de atacar a esta trabajadora con las armas más asquerosas y rastreras que uno pueda imaginar. Eso sí, finalmente, ha pedido perdón, no sé a instancias de quién, supongo que porque parece que, afortunadamente, Teresa se salva y temerá todas las demandas que esta mujer podría poner.

Como ya han corrido ríos de tinta (o bits) hablando de semejante personaje y mi idea al empezar a escribir este artículo era la de proporcionar una lectura agradable y relajada, voy a pasar de estos indeseables y a centrarme en una pregunta que yo misma me hago desde aquí y yo misma voy a tratar de dar una respuesta: ¿cómo pueden ayudar las matemáticas a la detección, prevención y cura de las enfermedades?

No pretendo ser exhaustiva en la respuesta. Sería muy largo de leer y muy complicado en algunos puntos para lectores alógenos a la materia. Solo pretendo dar unas pistas de qué tipo de matemáticas son útiles en esta empresa.

Empecemos por el principio. Aunque el uso de modelos matemáticos en el estudio de epidemias se sistematizó sobre los años veinte del siglo pasado, podemos encontrar aplicaciones de conceptos matemáticos mucho antes. Hay quien señala a John Graunt, un mercero de Londres (sí, un señor que se dedicaba a la mercería), del siglo XVII, como el precursor de la epidemiología. De hecho, se le considera el primer bioestadístico de la historia. Sus actividades como comerciante le permitían el acceso a los boletines con los datos de las muertes de Londres , que incluían la edad y el domicilio del fallecido y el bueno de Graunt confeccionaba con ellos tablas de datos que podían ayudar a predecir una posible epidemia, por ejemplo, de peste. Para que vean.

También uno de los Bernouilli, concretamente Daniel, ya en el siglo XVIII, diseñó un modelo matemático para convencer de la importancia de vacunarse contra la viruela. Se ve que ya había algunos iluminados antivacunas en aquella época…

Pero, si me lo permiten, la aplicación más importante de conceptos matemáticos, geométricos concretamente, al estudio de una epidemia lo encontramos en 1854, cuando John Snow (que no tiene nada que ver ni con juegos ni con tronos), el padre de la epidemiología moderna descubrió que el cólera (del que había un brote en Londres por aquella época) se transmitía a través del agua, y no a través del contacto físico o el ambiente como se pensaba hasta entonces. ¿Cómo llegó el doctor Snow a esa conclusión? Con mucho trabajo, observaciones y deducciones acertadas, pero en pocas palabras, el doctor Snow percibió que, salvo unos pocos casos, todas las muertes por cólera estaban relativamente concentradas geográficamente. Supo además que las muertes ocurridas fuera de esa determinada zona fueron de personas que habían visitado la casa de un familiar muerto por cólera en la zona chunga o, incluso, la de una señora que, al mudarse a otra zona de la ciudad, pedía a un vendedor ambulante que le llevase a su nueva casa agua de la fuente de Broad Street, que le sentaba muy bien. Y tanto. Ese agua sí que tenía memoria, sí, señor. Recordaba haber estado en contacto con las caquitas de un bebé enfermo de cólera.

Con esto, lo que hizo John Snow, fue dibujar en un plano lo que más tarde se conoció como regiones de Voronoide cada fuente de la ciudad. La región de Voronoi de cada fuente (él no las llamó así porque, entre otros detalles, Voronoi aún no había nacido) correspondía con las casas de la ciudad que estaban más cerca de esa fuente que de ninguna otra y, por lo tanto, eran los habitantes de dichas casas los presuntos usuarios de la fuente correspondiente por criterios de cercanía. El doctor Snow descubrió que, efectivamente, la mayoría de las muertes se habían producido en la región de Voronoi de la fuente de Broad Street. Cerró la fuente y terminó con la epidemia. De paso descubrió, como hemos dicho, que el cólera se trasmitía a través del agua. Anda. Alucinante, ¿no? Si les pica la curiosidad sobre otras aplicaciones del diagrama de Voronoi, aunque supongo que ya intuyen la de asignar así las zonas de reparto de, por ejemplo, una cadena de pizzerías, les invito a leeresto que escribí hace un tiempo.

Esto fue en el siglo XIX y la matemática involucrada fue la geometría. Una de las ramas que más me gustan a mí, por cierto, aunque esta información sea desde todo punto de vista irrelevante.

Sin duda, los modelos matemáticos más usados en el estudio de la propagación de enfermedades llegan de la mano de las ecuaciones diferenciales y estos aparecieron ya en el siglo XX, alrededor de 1927 y de la mano, o de las mentes de A.G. McKendrick y W. O. Kermack. Si se siente tentado de abandonar la lectura en este momento por lo de las ecuaciones diferenciales, por favor, no lo haga, deme la oportunidad de tratar de explicarlo de la forma más sencilla que pueda. Los que sean doctos en la materia, espero sepan disculpar la falta de formalismo de la explicación.

Una ecuación no es más que una expresión matemática en la que aparece uno (o varios) valores desconocidos,la sospechosa letra x. Como le cuento a los niños, es una letra que se esconde en la ecuación y lo que hacemos los matemáticos es proporcionar estrategias para desenmascararla. Una ecuación muy simple sería, por ejemplo:

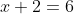
Se deduce sin mucha dificultad que en este caso, la x debe valer 4. Eso es una ecuación. Cuando la ecuación es diferencial, lo que se esconde no es un número, como el 4 en la ecuación anterior, sino una función.

Ajá, existen ecuaciones cuyas incógnitas son funciones, no números. Por ejemplo, si me dicen que resuelva la siguiente ecuación (en la que t no es una incógnita, la incógnita es la función f(t) que, lógicamente, será una expresión que dependa de t y no un número como en el ejemplo anterior):

La solución a la anterior ecuación sería la función f(t)=2t, solo tienen que sustituir f(t) por 2t en la ecuación para comprobarlo. Esto es una ecuación funcional, porque la incógnita es una función. Hay muchas ecuaciones funcionales un poco más complicadas que esta que tienen mucha importancia en matemáticas, pero no las necesitamos ahora.

Creo que ya estamos en condiciones de explicar qué es una ecuación diferencial, esas que nos sirven para describir y estudiar las epidemias y otros fenómenos de propagación. Si en la ecuación funcional además de aparecer f(t) aparece su derivada (que es la función que nos ayuda a saber cómo crece el valor de f(t) al crecer el valor de t y que escribimos como df(t)/dt), la ecuación es diferencial. Ya está. Por ejemplo, si tenemos la siguiente ecuación diferencial:

la solución a esa ecuación será una función f(t) que sea igual que su derivada. Esa función es 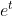 por ser la única función que coincide con su derivada y con su integral. De ahí el manido chiste de que  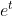se intenta integrar en las fiestas pero se queda igual.

Vamos con las epidemias. Uno de los modelos (de ecuaciones diferenciales) más simples se conoce como elmodelo S.I.R, por estudiar la variación de tres funciones: S (en realidad, S(t)) que será el número de individuos sanos y, por lo tanto, susceptibles de ser infectados; la I, o mejor dicho, I(t) es el número de individuosinfectados; y R (o R(t)) que es el número de individuos recuperados (bien porque se han curado y son inmunes, o bien porque han muerto, pero ya no son ni infectados ni susceptibles de enfermar). Vamos, que la población total del área en estudio será

Las ecuaciones de este modelo (las voy a poner pero no se me asusten) son las siguientes:

Como ven, la variación de individuos susceptibles, dS/dt, está en relación inversa con el número de infectados (I), cuando más se infecten menos quedan sanos; si se fijan en la segunda ecuación, el número de recuperados depende directamente del número de infectados (para recuperarse hay que infectarse primero).

Pero fijémonos en la tercera ecuación, la que nos dice el ritmo de variación de I, dI/dt, es decir, cómo crece o decrece el número de infectados. Si sacamos I como factor común en el miembro de la izquierda, podemos simplificar la explicación diciendo que la variación de I es un cierto valor R (que ese es el difícil de calcular) por el número de infectados I.

Resumiendo mucho todo lo anterior: cuando tratamos de estudiar una epidemia definimos la función, I(t), que nos dice para cada valor de t, para cada instante de tiempo t, cuántos afectados por la enfermedad hay:

I(t)= número de afectados por la enfermedad en el instante t

Para estudiar cómo irá avanzando la enfermedad en número de contagiados, lo que nos interesa saber es cómo va creciendo esta I(t) con el paso del tiempo. Eso, como hemos dicho unas línea más arriba, lo mide la derivada de I(t) respecto al tiempo, o sea dI(I)/dt (no se asusten, no tienen que saber derivar para seguir esta historia). Lo que, en muy pocas palabras y en un modelo muy muy simplificado, hacen los modelos matemáticos que estudian las epidemias es calcular (en función de un montón de parámetros, algunos muy difíciles de conocer y, por tanto, solo se usan valores estimados) ese valor R que describe el crecimiento de I(t) con la siguiente ecuación:

Esto es una simplificación, muy simplificada, de un modelo de propagación. La solución de esta ecuación funcional será 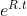, que es un función que crece muy rápido si R es mayor que 1.

Luego lo que tratan de medir los investigadores de la epidemia en cuestión es cuánto vale R para cada brote en estudio. Según uno de los últimos estudios realizados para el caso del actual brote de ébola, ese parámetro Restá cercano a 2, lo cual es bastante chungo, pero por debajo de 2, lo cual es, en alguna medida esperanzador. Evidentemente, el valor del parámetro R también va cambiando con el tiempo y aunque al principio vaya creciendo, con el tiempo empieza a disminuir por un efecto de «saturación», la población es finita (lo contrario de infinita, no delgada) y el virus se va quedando cada vez con menos gente a la que atacar. Pues bien, dependiendo de cómo y con qué parámetros se calcule ese valor R, existen diferentes modelos de ecuaciones diferenciales que estudian la propagación de la epidemia. Esto solo sirve para evaluar, si quieren, la urgencia con la que actuar y los medios que poner a disposición, pero no cura. Curar curan los médicos con ayuda de personal sanitario, como Teresa. Y no, no hay dietas milagrosas ni chuminás de esas que anuncian los magufoscontra el ébola. Ni contra el cáncer como dice una señora, Odile creo que se llama, que anda dando conferencias por España.

Aunque no lo he dicho, para los modelos basados en ecuaciones diferenciales, los que acabo de describir, se necesitan otras herramientas de las matemáticas: la estadística y el análisis numérico, por ejemplo. Necesarios para conocer valores relacionados con la enfermedad que nos permitan calcular y/o estimar el parámetro R.

Pero hay más matemáticas, claro que sí.

Una herramienta posiblemente menos conocida en el estudio y prevención de epidemias nos llega de la mano de la teoría de grafos. De grafos ya hemos hablado por esta casa pero, rápidamente, un grafo por ejemplo esFacebook, donde cada persona representa a un vértice (punto) y dibujamos una arista (línea) entre dos vértices si estos dos son amigos en la citada red social. Si lo piensan, sin tener Facebook, todos somos vértices de un grafo y las aristas representarían las relaciones personales que tenemos. Pues bien, existe un resultado en teoría de grafos, conocido como la paradoja de la amistad, que asegura que, si el grafo es suficientemente grande, tus amigos tienen en media más amigos que tú, contradiciendo aquello de que los amigos de tus amigos son tus amigos. Con esto en la mano, en campañas de vacunación (en el caso de epidemias para las que existe vacuna) se ha probado que es más eficiente elegidos inicialmente unos individuos aleatoriamente, que estos señalen a unos cuantos amigos suyos y así sucesivamente para conseguir una mayor eficiencia en la campaña. Bueno, esto ya los saben muchas empresas que te regalan tostadoras si mandas los nombres de unos cuantos amigos tuyos…

¿Qué más? Pues no infinito, pero sí mucho más. No me voy a extender más hoy, si veo que les interesó el tema podemos seguir otro día contando que, por ejemplo, desde el punto de vista del diagnóstico existen muchos trabajos que tratan de deducir automáticamente si alguien es susceptible de contraer una enfermedad a partir de imágenes obtenidas por un TAC (por cierto: para toda la cuestión de imágenes médicas se utilizan muchas matemáticas, entre otras, geometría computacional, para poder reconstruir las imágenes tridimensionales a partir de la información que se obtiene de la captura de ciertas señales). O también que desde el punto de vista del tratamiento se estudian modelizaciones matemáticas de tumores. Estas no permiten predecir el comportamiento de estos ante distintos tratamientos teniendo en cuenta la particularidades de cada paciente y así se pueden diseñar técnicas específicas e individualizadas que son mucho más eficaces y menos agresivas en la lucha contra dicha enfermedad. O, a nivel más microscópico, se estudia cómo se anudan las cadenas de ADN de algunos virus, pura topología, porque en función de dichos nudos varía su comportamiento y se podrán tratar de una forma u otra.

Ahora sí, termino. Solo quiero dejarles este enlace a un trabajo que modela desde el punto de vista matemático el avance de un ataque zombi porque siendo lectores de Jot Down, posiblemente sean demasiado frikies para resistir la tentación de echarle un vistazo.

http://www.jotdown.es/